Introduction
A complex number is an extended version of real number in the form
x + iy; 𝑥∈ℝ
Euler (1707 – 1783) introduced the imaginary unit ‘i’ (read as iota) for √-1 with property
![]()
Therefore, imaginary unit i is the solution of an equation
![]()
Acomplex is written in the STANDARD form as z = x+iy where x and y are real numbers
Drag the point for intaraction : 👇
Note
- The cartesian form of complex number can be written z=x+iy [standard form] or z=(x,y) [order pair form]
- In z = (x,y,), x is real part denoted as Re (z), and y is imaginary part denoted as Im (z)
In z = (x,y), Re (z) = x and Im (z) =y - A complex number z = x+iy, is purely real if y = 0 i.e. Re (z) = 0, and purely imaginary if x = 0 i.e. Im (z) = 0.
- A complex number z = x+iy, is zero if x = y = 0 i.e. Re (z) = Im (z) = 0
The introduction of complex numbers gives rise to the fundamental theorem of algebra. In the 16th century, Italian mathematician Gerolamo Cardano used complex numbers to find solutions to cubic equations.
Then Italian mathematician Rafael Bombelli developed the rules for addition, subtraction, multiplication, and division of complex numbers. A more abstract formalism for complex numbers was developed by the Irish mathematician William Rowan Hamilton.
Meaning of i
In the complex number system, i is called imaginary unit. Tthe value of i is (0, 1). Thus, we can write i=(0,1).
If we expand a complex number z=(x,y) as z=(1,0)x+(0,1)y then (1,0) is unit of real part denoted by 1 and (0,1) is unit of imaginary part and denoted by i. Here i is imaginary unit with
![]() .
.
A complex number is visually represented in Argand diagram. Here i is operator giving anticlockwise quarter turn such that ![]() .
.
NOTE
- We should NOT mean i as non-existence number nor a number that exist only in imagination
- i is a number that denotes imaginary unit (0,1)
- i is an anticlockwise quarter turn operator for (x,y), thus
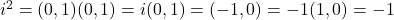
Positive powers of i
In general, for any integer k,
![]() .
.
For example:
![]()
The verification on the positive powers of i are as follows.
![]()
![]()
![]()
![]()
![]() and so on
and so on
Absolute Value
In a complex number
![]()
The absolute value is Modulus, a non-negative real number denoted by
| z | and defined by
![]()
Geometrically,
|𝑧| is distance of z from origin
Drag the point for intaraction : 👇
Note
Due to order property, z1 <z2 is meaningless unless z1 and z2 both are real.
However,| z1 | <| z2 | means z1 is closer than z2.
Distance between ![]() and
and ![]() is denoted by
is denoted by
![]()
and defined by
![]()
NOTE:
![]()
Conjugate
The conjugate of a complex number z=x+iy is denoted ![]() and defined by
and defined by
![]()
Geometrically, ![]() is reflection of
is reflection of ![]() on real axis
on real axis
Drag the point for intaraction : 👇
Properties of Conjugate numbers
- If
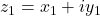 and
and 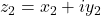 then
then 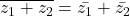
Proof
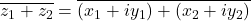
or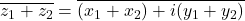
or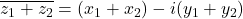
or
or
- The sum of a complex number z and its conjugate
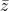 is twice of its real part
is twice of its real part
Proof
If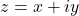 be a complex number then
be a complex number then 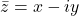 , where
, where
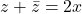
or
or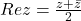
- The difference of z and its conjugate
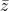 is twice of its imaginary part
is twice of its imaginary part
Proof
If z=x+iy be a complex number then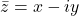 , where
, where

or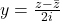
or
- The real and imaginary parts of a complex number can be extracted using its conjugate
Theorem: An important property
Let z=x+iy be a complex number then ![]()
Proof
Given z=x+iy be a complex number, then ![]() .
.
Now,
![]()
or
![]()
or
![]() (i)
(i)
Also
![]()
or
![]() (ii)
(ii)
From (i) and (ii), we get
![]()
Question
Theorem: Triangle inequality: 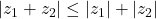
Proof>br> We know that
![]()
or
![]()
or
![]()
or
![]()
or
![]()
or
![]()
or
![]()
or
![]()
or
![]()
or
![]()
This completes the proof.
Corollary
-

Proof
or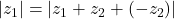
or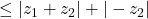
or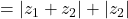
Thus,
-

Proof
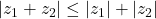
Now, replacing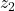 by
by  we get
we get
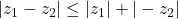
Thus,
-

Proof

Now, replacing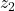 by
by  we get
we get
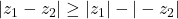
Thus,
Algebra of complex number
Complex plane looks like an ordinary two-dimensional plane of z=( x,y ), but z=( x,y ) is a single number losing order axioms. Fundamental operations on complex number are defined as below.
- Equality
Two complex numbers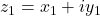 and
and 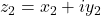 are equal if
are equal if
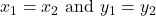
- Addition
Sum of two complex numbers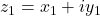 and
and 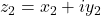 is defined as
is defined as

According to definition,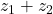 corresponds to resultant vector addition.
corresponds to resultant vector addition.
- Multiplication
Product/multiplication of two complex numbers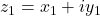 and
and 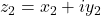 is defined as
is defined as
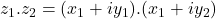
or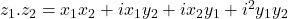
or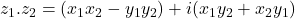
The product is neither scalar nor the vector product of ordinary vector analysis. This departure is due to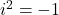
Also, complex number C is a field. Thus, the complex number satisfy all Field axioms as below.
- Closer:

- Additive associative
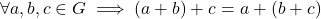
- Additive identity

Additive identity (0,0) - Additive Inverse
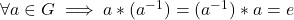
Additive inverse of z=x+iy is -z=-x-iy - Additive commutative

- Distributive
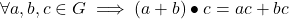
- Multiplicative associative
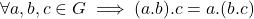
- Multiplicative identity

Multiplicative identity (1,0) - Multiplicative inverse
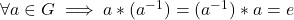
Multiplicative inverse of non-zero complex number z=x+iy is
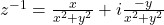
Proof
Let z=x+iy be non-zero complex number and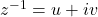 be its multiplicative inverse, then
be its multiplicative inverse, then
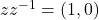
or
or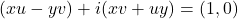
Comparing real and imaginary parts separately, we get
ux-vy=1 and uy+vx=0
Solving for u and v , we get
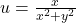 and
and 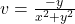
Hence,
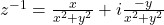
- Multiplicative commutative

Algebric Structure
| Axioms | Structure | Example |
| 1-2 | Semi Group | Example |
| 1-3 | Monoid | Example |
| 1-4 | Group | Example |
| 1-5 | Abelian Group | Example |
| 1-6 | Ring | Example |
| 1-7 | Assocoative Ring | Example |
| 1-8 | Assocoative Ring with Unity | Example |
| 1-9 | Division Ring (Skew Field) | Example |
| 1-10 | Field | Example |
Polar form
Drag the point for intaraction : 👇
Let ![]() be a complex number with magnitude r and amplitude
be a complex number with magnitude r and amplitude ![]() , then
, then
![]() and
and ![]()
Hence,
![]()
or
![]()
Thus, a complex number z=x+iy is represented by polar coordinate ![]() , as
, as
![]()
Here,
r is the length of z , and ![]() is argument of z with
is argument of z with
![]() , and
, and ![]()
Example
Find polar form of complex number z=-5+5i
Solution
Given that
z=-5+5i
or
z=5( -1+i)
or
![]()
or
![]()
The relevance of complex number in polar form is that multiplication and division are simpler with this form than the Cartesian form.
Let ![]() and
and ![]() be two complex numbers, then
be two complex numbers, then
![]()
Proof
Given that ![]() and
and ![]() . Thus
. Thus
![]()
or
![]()
or
![]()
or
![]()
or
![]()
or
![]()
Theorem
![]()
Proof
LetThus,
Note:
Any complex number z has infinite arguments; all differ by multiple of ![]() . The principal value is in the interval
. The principal value is in the interval ![]()
Some important property
- Let
 be two complex number then
be two complex number then 
The argument of product of two complex number is sum of their arguments.
Proof
Let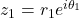 and
and 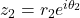 then
then
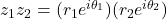
or
Hence,

- Let
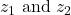 be two complex number then,
be two complex number then,
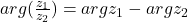
The argument of quotient of two complex number is difference of their arguments. - Argument of complex number of the form
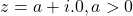 is 0
is 0 - Argument of complex number of the form
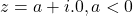 is
is 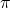
- Argument of complex number of the form
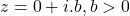 is
is 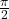
- Argument of complex number of the form
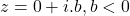 is
is 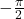
Drag the point for intaraction : 👇
If ![]() then show that
then show that ![]()
Question
Let ![]() be a complex number and its inverse is
be a complex number and its inverse is ![]() then
then
![]()
or
![]()
or
![]()
or
![]()
or
![]()
Thus,
![]()
Exponenrial Form
Euler’s formula establishes the fundamental relationship between the trigonometric functions and the complex exponential function. It states that for any real number x:
![]()
where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions.
When x = π, Euler’s formula evaluates to ![]() , which is known as Euler’s identity.
, which is known as Euler’s identity.
Given Euler’s exponential form,
![]()
Thus, complex number ![]() is defined as
is defined as
![]()
The significance of exponential form of complex number is that we can easily compute conjugate and inverse.
For example,
![]() and
and ![]()
Proof of the Formula
- Function Method
Consider the function f(θ) given by
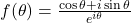
or
Differentiating gives by the product rule, we have

Thus, f(θ) is a constant.
Since f(0) = 1, then f(θ) = 1 for all θ, and thus

or
This completes the proof. - Series Method
We know that
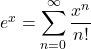
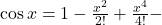
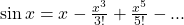
Using power series expansion, we get
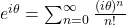
or
or
or
or
This completes the proof.
De-Moivre’s theorem
Let ![]() be a complex number then
be a complex number then ![]() where n is a positive integer.
where n is a positive integer.
Proof
- Case 1: n=1
Then
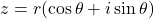
or
So,
or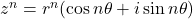 when n=1
when n=1
- Case 2: n=2
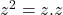
or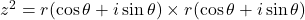
or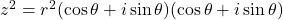
or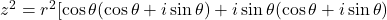
or![Rendered by QuickLaTeX.com z^2 = r^2 [\cos \theta \cos \theta +i\cos \theta\sin \theta +i\sin \theta\cos \theta -\cos \theta\sin \theta ]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-697d954335ebefda154553b83b828efc_l3.png)
or![Rendered by QuickLaTeX.com z^2 = r^2 [(\cos \theta \cos \theta-\sin \theta \sin \theta ) +i(\cos \theta\sin \theta +\sin \theta\cos \theta) ]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-4492fe8ef06118b65e3e91b0092ea619_l3.png)
or![Rendered by QuickLaTeX.com z^2 = r^2 [\cos (\theta +\theta) +i \sin (\theta+ \theta)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-763f2f436aca1e885e0d61c391b462c3_l3.png)
or![Rendered by QuickLaTeX.com z^2 = r^2 [\cos 2\theta +i \sin 2\theta]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-8e343acfc3f693fed9c6578134f2de93_l3.png)
So,
or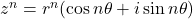 when n=2
when n=2
- Case 3: We assume the same formula is true for n = k, so we have

So,
or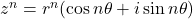 when n=k
when n=k
- Case 4: Now, we prove for n = k + 1,
![Rendered by QuickLaTeX.com [r(\cos\theta + i\sin\theta)]^{k + 1} = r^k(\cos\theta + i\sin\theta)^k r (\cos\theta + i\sin\theta)](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-8bf16e5f3f0fea65839bf0cdcee514a9_l3.png)
or![Rendered by QuickLaTeX.com [r(\cos\theta + i\sin\theta)]^{k + 1} = r^k(\cos(k\theta) + i\sin(k\theta)) r(\cos\theta + i\sin\theta)](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-bd5209dd102cb9f88de3d58f5c3b1429_l3.png)
or![Rendered by QuickLaTeX.com [r(\cos\theta + i\sin\theta)]^{k + 1} = r^{k+1}[(\cos(k\theta) \cos\theta-\sin(k\theta)\sin\theta )+i (\cos\theta\sin(k\theta) + \sin\theta\cos(k\theta))]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-2b57c67056f64db3cfc93a00197ee0a3_l3.png)
or![Rendered by QuickLaTeX.com [r(\cos\theta + i\sin\theta)]^{k + 1} =r^{k+1}[\cos(k\theta+\theta)+i \sin(k\theta+\theta )]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-1760bc3c865d7de725f1f65665d16dd4_l3.png)
or![Rendered by QuickLaTeX.com [r(\cos\theta + i\sin\theta)]^{k + 1} =r^{k+1}[\cos(k+1)\theta+i \sin(k+1)\theta]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-1d39bec89daa1bf6a29f775afb067774_l3.png)
So,
or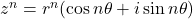 when n=k+1
when n=k+1
- Using case 1-case 4, for any number
 , we have
, we have
![Rendered by QuickLaTeX.com [r(\cos\theta + i\sin\theta)]^n =r^n[\cos(n\theta)+i \sin(n\theta)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-a92749346c8ca6fe9bb6b6d2abc8954f_l3.png)
Example 1
Compute ![]()
Solution
Since
![]()
or ![]()
We get
![]() and
and ![]()
Thus,
![]()
or
![]()
or
![]()
or
![]()
nth root of Complex number
If ![]() be a complex number then the nth root of z is
be a complex number then the nth root of z is
![]()
Proof
Given that Z is a complex number. Also let, nth root of Z is W such that ![]()
Now we have
![]()
or
![]()
or
![]()
or
![]()
Equating real and Imaginary parts, we get
![]() and
and ![]() and
and ![]()
or
![]() and
and ![]()
or
![]() and
and ![]()
Thus, nth root of ![]() is
is
![]()
or
![]()
square roots of i
Find the square roots of i
We know that
![]()
Solution
Since ![]() , we get
, we get
r=1 and ![]()
Hence the first square roots of i is
![]()
The second square root of i is
![]()