Statistics is the study of data. Data is collected resources that is translated into a meaningful information. Data is a measured values and it can be classified into four different perspectives. तथ्याङक शाश्त्र भनेको डाटाको अध्ययन गर्ने गणितको एउटा खण्ड हो। डाटा भन्नाले संकलन गरिएको कच्चा संसाधन हो जसलाई अर्थपूर्ण सुचनाको रुपमा मा प्रशोधन गर्नु पर्ने हुन्छ । समग्रमा, डाटा भन्नाले मापन गरिएको मान हो र जसलाई चार फरक दृष्टिकोणका आधारमा वर्गीकृत गर्न सकिन्छ।
- Based on collection (Primary and Secondary) संग्रहमा आधारित (प्राथमिक र माध्यमिक)
- Based on Scale/ Measurement (Nominal, Ordinal, Interval, Ratio) मापनमा आधारित (नाम बुझाउने, क्रम बुझाउने, अन्तराल बुझाउने, अनुपात बुझाउने)
- Based on nature (Qualitative and Quantitative) प्रकृतिका आधारित (गुणात्मक र मात्रात्मक)
- Based on distribution (Individual, Discrete, Continuous) बर्गिकरण \ वितरणका आधारमा (व्यक्तिगत, खण्डित, निरन्तर)
- Descriptive statistics
- Inferential statistics
Descriptive statistics
A statistics that collects, organize and summarize the information is called Descriptive statistics. For example bar graph and mean.Inferential statistics
A statistics that utilize current data and predicts it for future reference, is called inferential statistics. For example hypothesis test or regression analysis.Measure of Central tendency
Measure of central tendency लाई केन्द्रीय प्रवृत्तिको मापन भनिन्छ । यसले तथ्याङकको केन्द्रमा हुने प्रवृत्तिको एकल मान (डाटा सेटको प्रतिनिधि मान) लाई जनाउदछ जसले डाटाको सम्पूर्ण मात्रात्मक सेटको प्रतिनिधित्व गर्दछ। यस केन्द्रीय प्रवृत्तिको मापनलाई स्थान वा स्थितिको मापन पनि भनिन्छ, यसैलाई औसत मापन पनि भनिन्छ।
The Measure of central tendency is a statistic that summarizes the entire quantitative set of data in a single value (a representative value of the data set) having a tendency to concentrate somewhere in the center of the data. Therefore, the tendency of the observations to cluster in the central part of the data is called the central tendency. It measures the central location (or position) of data set. It is also known as average.
- केन्द्रीय प्रवृत्तिको मापन जहिले पनि डाटा सेटको दायरा भित्र पर्दछ। The Measure of central tendency lies somewhere within the range of the data set
- डाटा लाई फरक अर्डरमा पुनर्व्यवस्थित गर्दा केन्द्रीय प्रवृत्तिको मापनमा परिवर्तन हुदैन । The Measure of central tendency remain unchanged by a rearrangement of the data set
- मध्ययक (Mean)
- मध्यिका (Median), Quartile, Decile, Percentile
- रीत (Mode)}
Mean
Mean is measure of central tendency that utilize each and every data to give a single best value. The arithmetic mean or simply mean is also knows as average, which is obtained by dividing the sum of all the observations by total number of observations (summed).
It is denoted by ![]() and define as follows.
and define as follows.
| Individual data | Discrete data | Continuous data | |
| Arithmetic Mean | | ||
| Geometric Mean | | ||
| Harmonic Mean | | ||
| Weighted Mean | |
- अंकगणितिय मध्यक (AM) Arithmetic Mean
The arithmetic mean answers the question, “if all the quantities have same value, what is the value to achieve the same total?” The answer is AM. For example, let Ram has Rs 100 and Shyam has Rs 120, then the avarage amount is AM, which is answered by
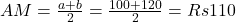
In the figure below, a+b is same as AM+AM. - ज्यामितीय मध्यक (GM) Geometric Mean
The geometric mean answers the question, “if all the quantities have same value, what is the value to achieve the same product?”. The geometric mean is a useful when we expect changes in data in percentages as rate of change or ratios. It is utilised in the field of finance for the purpose of determining average growth rates, which are also known as the compounded annual growth rate. For example, let Ram deposited Rs 100 in a bank, on which 80% growth in first year and 25% growth in second year, then the average profit is GM, which is answered by
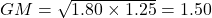 , the average growth is 50%
, the average growth is 50%
Please note that, the situation can NOT be explained by
In the figure below, a*b is same as GM*GM. - हार्मोनिक मध्यक (HM)Harmonic Mean
Harmonic Mean is used to calculate average speeds of various distances covered.For example, Let Ram traveled 100km with fuel efficiency 25KM per liter and next 100km with fuel efficiency 16KM per liter, then the average fuel efficiency is HM, which is answered by
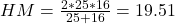
Please note that, the situation can NOT be explained by AM or GM
Because
The full efficiency for first 100 km is liter
liter
The full efficiency for second 100 km is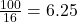 liter
liter
The total fuel efficiency is
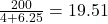
- भारित मध्यक (WM)Weighted Mean}
A weighted mean is a kind of average where some data points contribute more “weight” than others. If all the weights are equal, then the weighted mean equals the arithmetic mean.
Application of Mean
The mean is calculated from all data value, so it is affected by each and every value of data set. It is applicable if the data distribution represents- Quantitative data
- Closed ended
- Normally distributed data
Relation between AM, GM and HM
Let a and b are two non-negative numbers, then
-

 Arithmetic mean is greater than geometric mean and harmonic mean, and geometric mean is greater than harmonic mean.
Arithmetic mean is greater than geometric mean and harmonic mean, and geometric mean is greater than harmonic mean.
Let a and b are two non-negative numbers then,
![]()
The proof are as follows:
-
Now, we have
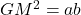
or
or
-
Now, we have
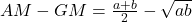
or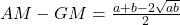
or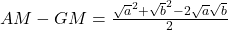
or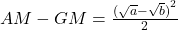
or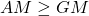 (1)
(1)
Similarly,
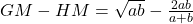
or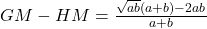
or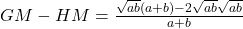
or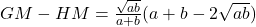
or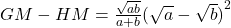
or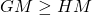 (2)
(2)
Combining (1) and (2), we get

Visualization of the proof
Let us suppose that a and b are two given numbers. Now, draw a semi circle with diameter a+b.
-
Visualization of AM
By the property of radius and diameter, we get that
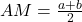
-
Visualization of GM
By the mean proportionality property (squaring a rectangle), we can obtain by using the property of similarity that, DQ is the geometric mean given by

-
Visualization of HM
By using proportionality, we get
Triangle ADQ and QDB are similar with AD=a, DB=b, so we have
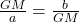
or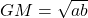
Again, by using the property of similarity on OCDE, we get that, QR is the harmonic mean given by
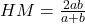
By using proportionality, we get
Triangle DRQ and ODQ are similar with QR=GM,QD= , OD=
, OD= , so we have
, so we have
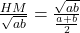
or
Example 1
Find the mean of the numbers 3, −7, 5, 13, −2
The sum of the numbers is
![]()
There are 5 numbers, so n=5.
Hence, the mean of the numbers is
![]()
Example 2
Find the mean of the wages from the following data| Wages | 50 | 70 | 90 | 110 | 130 | 150 |
| Number of Workers | 2 | 4 | 5 | 6 | 2 | 1 |
| Wages | Number of workers | |
| 50 | 2 | 100 |
| 70 | 4 | 280 |
| 90 | 5 | 450 |
| 110 | 6 | 660 |
| 130 | 2 | 260 |
| 150 | 1 | 150 |
Example 3
Find the average marks from the following data| Marks of the Students | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Number of Students | 20 | 50 | 55 | 40 | 15 |
| Marks of students | Mid value of marks | Number of students | |
| 0-20 | 10 | 20 | 200 |
| 20-40 | 30 | 50 | 1500 |
| 40-60 | 50 | 55 | 2750 |
| 60-80 | 70 | 40 | 2800 |
| 80-100 | 90 | 15 | 1350 |
Median
Median is a measure of central tendency that utilize middle portion of the data to give a single best value. The median is the middle value of the data series when the values are placed in order of magnitude (in ascending or descending order). Therefore, Median is not affected by extreme values. It is denoted by ![]() and define as follows.
and define as follows.
| Individual | Discrete | Continuous | |
| Median | | with |
- Sort the data in an ascending order.
- Find the middle number of the sorted data.
- If there’s an odd number of data, get the value exactly in the middle.
- If there’s an even number of data, get the mean of the two middle values.
- Qualitative data
- Open ended or Skewed data
Example 1
Find the median of the following wages(in hundreds): ![]()
Given wages (in hundreds) are
![]()
Arranging the wages in ascending order, we get
| 30 | 32 | 35 | 40 | 42 | 45 | 48 |
| 1st item | 2nd item | 3rd item | 4th item | 5th item | 6th item | 7th item |
Here, the number of data are n=7, thus, based on the formula, the Median is
![]() item
item
or ![]() item
item
or ![]() item
item
or ![]() hundreds
hundreds
Example 2
Find the median of the wages from the following data| Wages | 50 | 70 | 90 | 110 | 130 | 150 |
| Number of Workers | 2 | 4 | 5 | 6 | 2 | 1 |
| Wages | Number of Workers | Cumulative frequency |
| 50 | 2 | 2 |
| 70 | 4 | 6 |
| 90 | 5 | 11 |
| 110 | 6 | 17 |
| 130 | 2 | 19 |
| 150 | 1 | 20 |
or
or
or
Example 3
Find the median marks from the following data| Marks of the Students | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Number of Students | 20 | 50 | 55 | 40 | 15 |
| Marks of the Students | Number of Students | Cumulative frequency |
| 0-20 | 20 | 20 |
| 20-40 | 50 | 70 |
| 40-60 | 55 | 125 |
| 60-80 | 40 | 165 |
| 80-100 | 15 | 180 |
Here, the number of data are ![]() , thus, based on the formula, the Median class is
, thus, based on the formula, the Median class is
Md Class![]() item
item
or Md Class![]() item
item
or Md Class![]() item
item
Here, ![]() item lies in the
item lies in the ![]() of 125, thus
of 125, thus
![]()
Hence, the Median is
![]()
or ![]()
Example 4
Find the median marks from the following data| Marks of the Students | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Number of Students | 2 | 3 | 5 | 4 | 6 |
| Marks of the Students | Number of Students | Cumulative frequency |
| 0-20 | 2 | 2 |
| 20-40 | 3 | 5 |
| 40-60 | 5 | 10 |
| 60-80 | 4 | 14 |
| 80-100 | 6 | 20 |
Here, the number of data are ![]() , thus, based on the formula, the Median class is
, thus, based on the formula, the Median class is
Md Class![]() item
item
or Md Class ![]() item
item
or Md Class ![]() item
item
Here, ![]() item lies in the
item lies in the ![]() of 10, thus
of 10, thus
![]()
Hence, the Median is
![]()
or ![]()
NOTE
In the example above, student may ask that the median ![]() does not lie in the class
does not lie in the class ![]() as instructed for inclusive data groupings, teaches need to encourage the usual rules for computing.
as instructed for inclusive data groupings, teaches need to encourage the usual rules for computing.
Quartile, Decile and Percentile
The formula for Quartile, Decile and Percentile are similar as of Median.| Individual | Discrete | Continuous | |
| Quartile k=1,2,3 | | with | |
| Decile | | with | |
| Percentile | | with |
Mode
The concept of mode, as a measure of central tendency, is preferable when it is desired to know the most typical value, e.g., the most common size of shoes, the most common size of a ready-made garment, the most common size of income, the most common size of pocket expenditure of a college student, the most common size of a family in a locality, the most common duration of cure of viral-fever, the most popular candidate in an election, etc.
Thus, Mode is a measure of central tendency that utilize fashionable (most repeated data) information to give a single best value. So, Mode is an average value which occurs most frequently in a set of data i.e. it indicates the most frequent (common) results. It is not affected by every values. It is denoted by ![]() and define as follows.
and define as follows.
| Individual | Discrete | Continuous | |
| Mode | Repeated data | Repeated data/ Table analysis | |
- Frequency related data
- Fashionable data
Example 1
Find the mode value of the following data:Given data set are
In frequency table, the data set becomes
| X | 3 | 5 | 7 | 12 | 13 | 14 | 20 | 23 | 29 | 39 | 40 | 56 |
| f | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 1 | 1 | 1 |
Example 2
Find the Mode of the wages from the following data\par| Wages | 50 | 70 | 90 | 110 | 130 | 150 |
| Number of Workers | 2 | 4 | 5 | 6 | 2 | 1 |
Example 3
Find the Mode of from the following data| Wages | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| Number of Workers | 4 | 12 | 15 | 18 | 32 | 14 | 13 |
Being highest frequency 4, the model class is ![]() . Thus,
. Thus,
![]()
Hence, using formula, the Mode is
![]()
or ![]()
Analytical method to find the Mode
If the frequency distribution is regular, then mode is determined by the value corresponding to maximum frequency. There may be a situation where frequency distribution is NOT regular, means the concentration of observations around a value having maximum frequency is less than the concentration of observations around some other value. In such a situation, mode cannot be determined by the use of maximum frequency criterion. Further, there may be concentration of observations around more than one value of the variable and, accordingly, the distribution is said to be bi-modal or multi-modal depending upon whether it is around two or more than two values. In such cases, we use analytical method (also called tabular or grouping or empirical method) to find the Mode.
दिएको श्रेणिमा Mode अस्पष्ट भएमा वा तलका निम्न अवस्थामा यो बिधीको प्रयोग गरिन्छ ।
- highest frequency सख्या एक भन्दा बढी भएमा
- highest frequency तथ्याङकको सुरु वा अन्यतिर भएमाा
- highest frequency को वरिपरि ठुला frequency भएमाा
- frequency को अनियमित घटबढ भएमाा
Example 4
Find the Mode of from the following data| Wages | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| Number of Workers | 1 | 5 | 17 | 22 | 21 | 20 | 9 | 3 | 4 |
Here, the maximum frequency is ![]() , however three are big frequencies around 22, thus we use analytical method to find the Mode.
, however three are big frequencies around 22, thus we use analytical method to find the Mode.
Hence, based on the rule, the analytic table is given as below.
| Wages | | 1st + 2nd | 2nd+ 3rd | 1st+2nd+3rd | 2nd+3rd+4th | 3rd+4th+5th |
| 10 | 1 | |||||
| 6 | ||||||
| 20 | 5 | 23 | ||||
| 22 | ||||||
| 30 | 17 | 44 | ||||
| 39 | ||||||
| 40 | 22 | 60 | ||||
| 43 | ||||||
| 50 | 21 | 63 | ||||
| 41 | ||||||
| 60 | 20 | 50 | ||||
| 29 | ||||||
| 70 | 9 | 32 | ||||
| 12 | ||||||
| 80 | 3 | 16 | ||||
| 7 | ||||||
| 90 | 4 |
- Prepare a table consisting of 7 column, 1st column for X, 2nd column for frequencies of X.
- In third column, add the frequencies, starting from the top and grouped in twos.
- In forth column, add the frequencies, starting from the second and grouped in twos.
- In fifth column, add the frequencies, starting from the top and grouped in threes .
- In sixth column, add frequencies, starting from the top second and grouped in threes.
- In seventh column, add the frequencies, starting from the top third and grouped in threes.
- Finally, prepare frequency chart based on the analytic table
| Column | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| 1 | 1 | ||||||||
| 2 | 1 | 1 | |||||||
| 3 | 1 | 1 | |||||||
| 4 | 1 | 1 | 1 | ||||||
| 5 | 1 | 1 | 1 | ||||||
| 6 | 1 | 1 | 1 | ||||||
| Total | 2 | 4 | 5 | 3 | 1 |
Relation between Mean Median and Mode
A distribution in which the values of mean, median and mode coincide (i.e. mean = median = mode) is known as a symmetrical distribution.
Conversely, when values of mean, median and mode are not equal the distribution is known as asymmetrical or skewed distribution. In moderately skewed or asymmetrical distribution, a very important relationship exists among these three measures of central tendency. In such distributions
Mode = 3 Median – 2 Mean