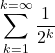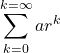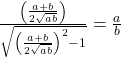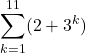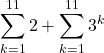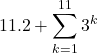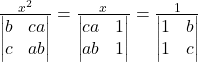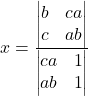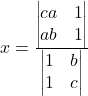In mathematics, the word, “sequence” we usually mean a ordered collection with an identified first member, second member, third member and so on. is also called progression (AP).
Introduction
Sequence is a pattern of ordered numbers. Since the numbers follow a pattern, we can relate each number to its numerical position with a rule. Such a rule is called sequence. Each
number in a sequence is a term of the sequence.
Presumably, a sequence continues by following the pattern that first few “terms”
suggest. To understand the pattern more explicitely, it is also useful to think of a sequence
as a function.
Thus,
So, a real-valued function defined on N = {1, 2, 3, . . .} is a
sequence.
The range of the function is
real numbers, the term of sequences
Mathematically, it is written as
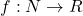 .
.
A sequence can be defined with two different ways
- Recursive definition (Syntactic definition), Implicit definition
- Formal definition (Semantic definition), Explicit definition
Recursive definition
A sequence can be described by comparing each term to the one that comes before it, i.e., by defining the later term in relationto previous terms. Such rule of describing sequence is called recursive definition. The recursive definition contains two parts. twwo parts, the initial condition and definition. For example, in a sequence
133,130,127,124,…,
each term after the first term is equal to three less than the previous term.
Therefore, a recursive definition for this sequence is as follows
- an initial condition (the value of the first term): a1=133
- a recursive definition (relates each term after the first term to the one before it): an=an-1-3 for n>1
Example 1
Writing a recursive definition for a sequence
The number of blocks in two dimensional pyramid is a sequence that follows a recursive formula. What is the recursive definition of the sequence?
The solution is as follows.
- Let us count the number of blocks in each pyramid: it is 1,3,6,10,….
- Now, subtract consecutive terms to find out what happens from one term to the next
a2-a1=3-1=2
a
3-a2=6-3=3
a
4-a3=10-6=4
- Now, use n to express the relationship between successive terms
a
n-an-1=n
- To write the recursive definition, state the initial condition and the recursive formula
a
1=1 and an=an-1+n
Example 2
What is the 100th term of the pyramid sequence in the example given below?
Solution
To find the explicit formula, expand the first few terms of the pyramid sequence. which is as below.
| a1 |
a2 |
a3 |
a4 |
… |
an |
| 1 |
3 |
6 |
10 |
… |
an |
| 1 |
1+2 |
1+2+3 |
1+2+3+4 |
… |
1+=2+3+4+…+n |
Therefore,
a
n=1+2+3+4+—+(n-2)+(n-1)+n (1)
Writing in reverse order, we get
a n=n+(n-1)+(n-2)+…+4+3+2+1 (2)
Adding (1) and (2), we get
| an |
=1 |
+2 |
3 |
+—+ |
(n-2) |
+(n-1) |
+n |
| an |
=n |
+(n-1) |
+(n-2) |
+—+ |
+3 |
+2 |
+1 |
| 2an |
=(n+1) |
+(n+1) |
+(n+1) |
+—+ |
+(n+1) |
+(n+1) |
+(n+1) |
| 2an |
=n(n+1) |
| an |
=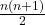 |
Therefore, the explicit formula, for this sequence is
a
n=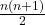
Now, we substitute n by 100 to find the 100th term. Which is
a
n=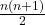
or
a
100=
or
a
100=5050
Now, we define sequence mathematically.
Semantic Definition
A sequence is a function defined on the set  . For example, f(an)=3an. There are different types of such sequences. Among them we discuss three basic types of sequence in the following section.
. For example, f(an)=3an. There are different types of such sequences. Among them we discuss three basic types of sequence in the following section.
- Arithmetic sequence
- Geometric sequence
- Harmonic sequence
Arithmetic Sequence
An arithmetic sequence is a list of numbers with a definite pattern based on addition. If you take any number in the sequence then subtract it by the previous one, and the result is always the same or constant then it is an arithmetic sequence.
In the arithemetic sequence
The constant difference in all pairs of consecutive or successive numbers is called the common difference. It is denoted by the letter d.
Please note that
Difference here means the second minus the first. We add the common difference to go from one term to
another.
Therefore,
An arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant.
For example,
the sequence 5, 7, 9, 11, 13, 15, . . . is an arithmetic progression with common
difference of 2.
General term of arithmetic sequence
An arithmetic sequence with a starting value  and common difference
and common difference  is a sequence of the form
is a sequence of the form
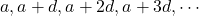
A recursive definition for this sequence has two parts
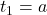 : initial condition
: initial condition
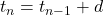 for n>1:recursive formula
for n>1:recursive formula
Therefore, an semantic definition for this sequence is a single formula as general terms given following calulations
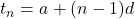 for n > 1
for n > 1
Proof.
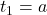
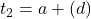
or 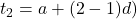
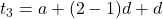
or 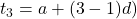

or 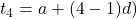
Similarly,
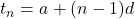 for n > 1
for n > 1
Arithmetic mean
Let a, b, and c are three terms in an arithmetic sequence, then b is called Arithemetic mean of a and c.
In this case
, first two terms a and b will have the difference which will be equal to the next two terms b and c.
So we can
Thus,
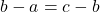 .
.
Rearranging the terms, we get
or
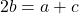
or
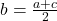
Arithmetic Series
An arithmetic series is the sum of the terms of an arithmetic sequence, denoted by 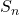
To find the explicit formula for the Sn: Sum of arithmetic sequence up to n th term, we write
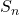 | =a | +(a+d) | +(a+2d) | +… | +[a+(n-2)d] | +[a+(n-1)d] |
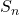 | =[a+(n-1)d] | +[a+(n-2)d] | +… | +(a+2d) | +(a+d) | +a |
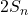 | =[2a+(n-1)d] | +[2a+(n-1)d] | +… | +… | +[2a+(n-1)d] | +[2a+(n-1)d] |
|
Thus
![Rendered by QuickLaTeX.com 2S_n=n[2a+(n-1)d])](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-910686debff500b1f22c1ed58187c3d3_l3.png)
or
![Rendered by QuickLaTeX.com S_n=\frac{n}{2}[2a+(n-1)d]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-c2289661094c4c21402dd01dc2c48f83_l3.png)
Example 3
If the first term of an AP is 67 and the common difference is -13, find the sum of the first 20 terms.
Here, a = 67 and d= -13, thus
Sn = ![Rendered by QuickLaTeX.com \frac{n}{2}[2a+(n-1)d]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-9812065ddf4337c09b7815550576b216_l3.png)
or
Sn = ![Rendered by QuickLaTeX.com \frac{20}{2}[2 \times 67+(20-1)(-13)]=-1130](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-238d997c6d97861e27abce0aa006f12d_l3.png)
So, the sum of first 20 terms is -1130.
Example 4
[Modeling]:Look at the figure below. The length of the side of each cube is 1cm. Copy the figure in isometric dot paper Based on the pattern
- Draw Figure no. 4 of this pattern on the dot paper
- Find the volume of the four Figures
- What would be the volume of Figure no. 12 of this pattern
- Write an equation to represent the volume of Figure n
Example 5
Show that sum of first n odd natural number is Sn=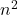
Here, a=1,d=2, thus the sum is
Sn=![Rendered by QuickLaTeX.com \frac{n}{2} [2a+(n-1)d]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-7e0d01436c2e0e628ca2c592a1adb728_l3.png)
or
Sn=![Rendered by QuickLaTeX.com \frac{n}{2} [2.1+(n-1)2]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-9651151e64371346292043b61567a7d5_l3.png)
or
Sn=![Rendered by QuickLaTeX.com \frac{n}{2} [2+2n-2]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-6f7f5949c089fada8e2c2ce45a9a4b47_l3.png)
or
Sn=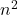
Example 6
Show that sum of first n even natural number is Sn=n(n+1)
Here, a=2,d=2, thus the sum is
Sn=![Rendered by QuickLaTeX.com \frac{n}{2} [2a+(n-1)d]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-7e0d01436c2e0e628ca2c592a1adb728_l3.png)
or
Sn=![Rendered by QuickLaTeX.com \frac{n}{2} [2.2+(n-1)2]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-08701b92eca2fbb9cddbcf5f8d722bad_l3.png)
or
Sn=![Rendered by QuickLaTeX.com \frac{n}{2} [4+2n-2]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-b1dc061f093442a7e319ecad99e80bfa_l3.png)
or
Sn=n(n+1)
Geometric sequence
Euclid’s book The Elements (300 BC, Book VIII) introduces a “geometric progression” as a progression in which the ratio of any element to the previous element is a constant.
The Greeks, over two thousand years ago, considered sequences such as
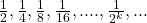
and their sums, such as
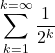
The sum, above, at any finite step, is always less than the number 1.
Since the sum is less than 1 at any finite step , we can conclude that the series converges in the limit to 1
Does a series have a sum?
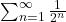
Answer
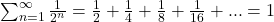
The sum of the series is 1.
The visualization is as follows
Imagine that we paint a blank canvas in steps. At each step, we paint half of the unpainted area. The total area painted after
“n” steps is therefore the “n”th partial sum
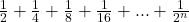
The total area remaining unpainted is
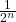
After an infinite number of steps we will have painted all of the canvas, of which the area is 1.
Geometric sequence
An geometric sequence is a list of numbers with a definite pattern based on multiplication. If you take any number in the sequence then divide it by the previous one, and the result is always the same or constant then it is an geometric sequence.
In the geometric sequence,
The constant ratio in all pairs of consecutive or successive numbers in a sequence is called the common ratio. It is denoted by a letter r.
Please note that
Ratio here means the second divide the first. We use the common ratio to go from one term to another.
Therefore, a geometric sequence is a sequence of numbers in which the ratio between the consecutive terms is always constant. For instance,
the sequence 5, 15, 45,135, . . . is an geometric progression with common ratio of 3.
General term of geometric sequence
A geometric sequence with a starting value a and common ratio r is a sequence of the form
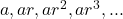
A recursive definition for this sequence has two parts
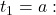 initial condition
initial condition
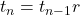 for n>1 recursive formula
for n>1 recursive formula
Therefore, an explicit definition for this sequence is a single formula as general terms given by
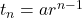 for n > 1
for n > 1
Example 1
When a ball bounces as shown below, the height of consecutive bounces become a geometric sequence. If 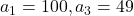 , thn what is the height of 5th bounce?
, thn what is the height of 5th bounce?
The height of the first and third bounces are given in the figure above.
Solution
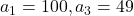
Use the explicit formula to relate a1 to a3 and to find r.
or
an=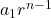
or
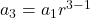
or
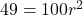
or
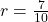
Find the fifth using explicit formula, thus we have
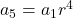
or
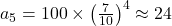
Geometric mean
In the geometric sequence, if a, b and c are three consecutive terms, then b is called geometric mean of a and b.
In this sequence, the first two terms a and b will have the ratio which will be equal to the next two terms b and c.
So we can say,
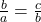
Rearranging the terms, we get
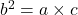
or

Geometric Series
A geometric series is the sum of the terms of an geometric sequence, denoted by 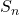
Let a geometric sequence is given by
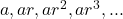
If we are adding up the terms of the geometric sequence given above, then we have a geometric sum or geometric series given by
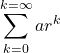
Method 1
The explicit formula for the sum of finite terms is given as below
Sum of geometric sequence up to n th term: 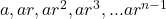 is written as
is written as
Sn=![Rendered by QuickLaTeX.com a+(a r)+(a r^2)+(a r^3)+---+[a r^{n-2}]+[a r^{n-1}]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-7c5558286ce5f5fb124d16d67b4f707f_l3.png)
Taking a common, we get
Sn=![Rendered by QuickLaTeX.com a[1+r+r^2+r^3+---+r^{n-2}+r^{n-1}]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-0bffa7667dbecd82ac12675f544fda5c_l3.png)
Multiplying by  , we get
, we get
Sn=![Rendered by QuickLaTeX.com a \frac{1-r}{1-r} [1+r+r^2+r^3+---+r^{n-2}+r^{n-1}]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-c4ea2b9bac6cbc71b1906a763098d529_l3.png)
or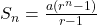
Method 2
Sum of geometric sequence up to n th term: 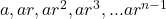 is written as
is written as
Sn=![Rendered by QuickLaTeX.com a+(a r)+(a r^2)+(a r^3)+---+[a r^{n-2}]+[a r^{n-1}]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-7c5558286ce5f5fb124d16d67b4f707f_l3.png)
Multiplying by r, we get
rSn=![Rendered by QuickLaTeX.com (a r)+(a r^2)+(a r^3)+---+[a r^{n-1}]+[a r^n]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-cfd630a1f95c4542e47074abfb9c4606_l3.png)
Substracting , we get
rSn-Sn=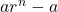
or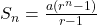
Infinite Sum
We know that, sum of the first n terms of a geometric series with first term a and
common ratio r is
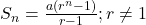
In the case when r has magnitude less than 1, the term  approaches 0 as n becomes
very large. So, in this case, the sequence of partial sums S1,S2,S3,... has a limit:
approaches 0 as n becomes
very large. So, in this case, the sequence of partial sums S1,S2,S3,... has a limit:
So,
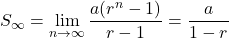
The limiting sum is usually referred to as the sum to infinity of the series and denoted
by S∞. Thus, for a geometric series with common ratio r such that |r | < 1, we have
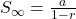
Example 2
A person saves NRs100 in a bank account at the beginning of each month. The bank offers a return of 12% compounded monthly.
(a) Determine the total amount saved after 12 months.
Solution
Let
Sn: Sum of geometric sequence up to n th term.
It is written as
Sn=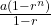
Based on the formula, the solution of above problem with
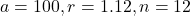
The solution is

Example 3
What is the sum of the finite geometric series 3+6+12+24+...+3072
Given that, the first term is 3, the common ratio is 2, and the nth term is 3072, therefore, we use explicit formula to find the n
an=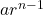
or
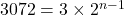
or
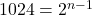
or
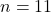
Therefore, the sum up to 11th term is
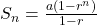
or
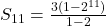
or
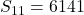
Harmonic sequence
In mathematics, a harmonic sequence formed by taking the reciprocals of an arithmetic progression.
The sequence 1,2,3,4,5,6,... is an arithmetic progression, so its reciprocals
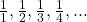
is a harmonic sequence.
If each term of an harmonic sequence is multiplied or divide by a constant, the sequence of the resulting number are also harmonic sequence. For example,
if
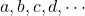
is harmonic sequence, then
- then
 is harmonic sequence where k is constant and
is harmonic sequence where k is constant and 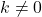
-
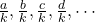 is a harmonic sequence where
is a harmonic sequence where 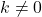
General term of Harmonic sequence
Let 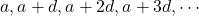 are the terms of arithemetic sequence
are the terms of arithemetic sequence
Then
terms of Harmonic sequence are given by
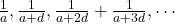
Now,
The nth term of the sequence is given by

Harmonic Mean
Harmonic mean is finding taking the reciprocal of the arithmetic mean of the reciprocals. The formula to calculate the harmonic mean is given by:
Harmonic Mean =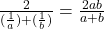
Where a,b are the values of arithmetic sequence.
Sum of Harmonic Series
If 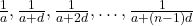 is given harmonic progression, the formula to find the sum of n terms in the harmonic progression is given by the formula:
is given harmonic progression, the formula to find the sum of n terms in the harmonic progression is given by the formula:
Sum of nth terms, ![Rendered by QuickLaTeX.com S_n= \frac{1}{d} \ln \left [ \frac{2a+(2n-1)d}{2a-d} \right ]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-282ab76899690679296abd6d655b9e97_l3.png)
where,
“a” is the first term of A.P
“d” is the common difference of A.P
“ln” is the natural logarithm
Proof
Given 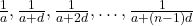 are in harmonic progression,
are in harmonic progression,
We set the values as follows,
a=1,d=1
Then, 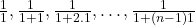 are the terms
are the terms
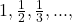 are the terms
are the terms
Now, the Riemann sum of the function 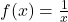 approximates the sum of the harmonic series given above
approximates the sum of the harmonic series given above
Therefore,
We set the values as follows,
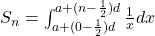
For any common difference,the formula becoms
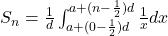
or 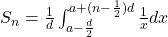
or ![Rendered by QuickLaTeX.com S_n= \frac{1}{d} \left [ \ln x \right]_{a-\frac{d}{2}}^{a+(n-\frac{1}{2})d}](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-ec8e5e5d222e8e3353398ab6474a76aa_l3.png)
or ![Rendered by QuickLaTeX.com S_n= \frac{1}{d} \ln \left [ \frac{2a+(2n-1)d}{2a-d} \right ]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-282ab76899690679296abd6d655b9e97_l3.png)
Therefore
The formula to find the sum of n terms in the harmonic progression is given by the formula:
Sum of nth terms, ![Rendered by QuickLaTeX.com S_n= \frac{1}{d} \ln \left [ \frac{2a+(2n-1)d}{2a-d} \right ]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-282ab76899690679296abd6d655b9e97_l3.png)
A.M, G.M, H.M and their relations
A finite sequence consisting more than two terms has one or more terms in between the first and last terms. Theses between terms are called means of the sequence. Precisely
- if a,b,c,d are in arithmetic sequence then b,c are arithmetic means (AM)
So, given n terms, the AM is
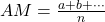
- item if a,b,c,d are in geometric sequence then b,c are geometric means (GM)
So, given n terms, the GM is
![Rendered by QuickLaTeX.com GM=\sqrt[n]{a \times \times \cdots }](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-ead7fee923b0656332f0adbc59b2e948_l3.png)
- if a,b,c,d are in harmonic sequence then b,c are harmonic means (HM)
So, given n terms, the HM is

Theorem 1
Given any two numbers a and b the AM, GM, and HM are as follows.
- AM=
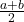
- GM=

- HM=
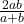
The proof are as follows:
- Let AM is the single mean between a and b, then
AM-a=b-AM
or
2AM=a+b
or
AM=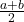
- Let GM is the single mean between a and b, then
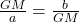
or
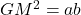
or
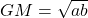
- Let HM is the single mean between a and b, then
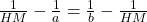
or
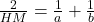
or

Theorem 2
Let a and b are two non-negative numbers, then
-

 Arithmetic mean is greater than geometric mean and harmonic mean, and geometric mean is greater than harmonic mean.
Arithmetic mean is greater than geometric mean and harmonic mean, and geometric mean is greater than harmonic mean.
Let a and b are two non-negative numbers then,
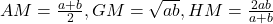
The proof are as follows:
-
Now, we have
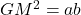
or

or

-
Now, we have
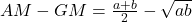
or
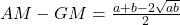
or
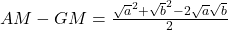
or
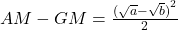
or
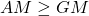 (1)
(1)
Similarly,
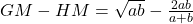
or
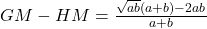
or
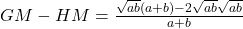
or
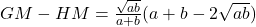
or
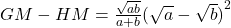
or
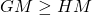 (2)
(2)
Combining (1) and (2), we get

Visualization of the proof
Let us suppose that a and b are two given numbers. Now, draw a semi circle with diameter a+b.
-
Visualization of AM
By the property of radius and diameter, we get that
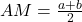
-
Visualization of GM
By the mean proportionality property (squaring a rectangle), we can obtain by using the property of similarity that, DQ is the geometric mean given by

-
Visualization of HM
By using proportionality, we get
Triangle ADQ and QDB are similar with AD=a, DB=b, so we have
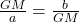
or 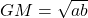
Again, by using the property of similarity on OCDE, we get that, QR is the harmonic mean given by
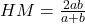
By using proportionality, we get
Triangle DRQ and ODQ are similar with QR=GM,QD= , OD=
, OD= , so we have
, so we have
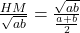
or 
Solved Example
Compare the sum of n terms of the series: 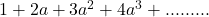 and
and 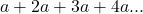 up to n term
up to n term
Solution
Given that
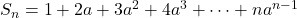
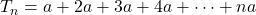
Now, substracting, we get
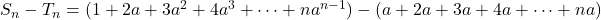
or 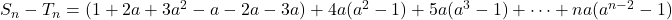
or 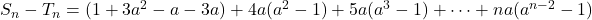
or 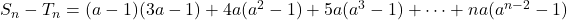
Case 1: If a=1, then
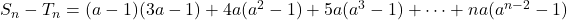
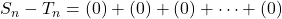
or 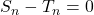
or 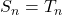 (1)
(1)
Case 1: If a >1, then
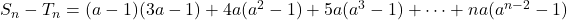
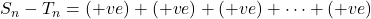
or 
or 
or 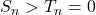 (2)
(2)
Thus, the comparision is
 if a =1
if a =1
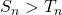 if a > 1
if a > 1
Exercise
- Integration to Investment and Growth: Determine the monthly repayments needed to repay a 100000 loan which is paid back over 25 years when the interest rate is 8% compounded annually[Ans: 780.66]
- Show that if three quantities form any two of the three sequences AS,GS,and HS then they also form the remaining third sequence
- The sum of three numbers in AP is 36. When the numbers are increased by 1,4,43 respectively, the resulting numbers are in GP, find the numbers.
- Divide 69 in three parts in AP and the product of first two parts is 483
- If a be the AM between b and c, b be the GM between c and a, then prove that c will be HM between a and b.
- Show that b^2 is greater than, equal to, or less than according as a,b,c are in AP, GP or HP
- If a and b are two positive numbers then prove that AM,GM,HM form GP.
- If the
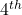 and
and 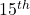 terms of an arithmetic series are 11 and 44 respectively then, find the sum of its first 20 terms. (Ans:610)
terms of an arithmetic series are 11 and 44 respectively then, find the sum of its first 20 terms. (Ans:610)
- Puja gets an employment of Rs.25000 in a month with an annual increment of Rs. 1500. How much does she earn in six years? Find her salary at 12^{th} year. (Ans: Rs.190500, Rs.41500)
- In a geometric series, if the sixth term is 16 times the second term and the sum of first seven terms is
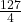 , then find the sum of the first 15 term. (Ans:
, then find the sum of the first 15 term. (Ans: 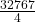 )
)
- There are 8 bags full of books. The numbers of books in each bag form a GP. If the
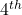 and
and 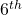 bags contain 24 and 96 books respectively, find the number of the books in the
bags contain 24 and 96 books respectively, find the number of the books in the 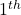 and last bags. ( Ans: 3, 384)
and last bags. ( Ans: 3, 384)
- One side fo a square is 10 cm . The mid point of its sides are joined to form another square, whose mid point are again joined t form one more square. The process is continued indefinitely. Find the sum of the areas of all the squares so formed. (Ans:200 square cm)
Exercise: Miscellaneous Exercise [NCERT, pg 147]
- If f is a function satisfying f (x +y) = f(x) f(y) for all x, y ∈ N such that
f(1) = 3 and
 ,find the value of n.
,find the value of n.
Solution 👉 Click Here
- The sum of some terms of G.P. is 315 whose first term and the common ratio are
5 and 2, respectively. Find the last term and the number of terms.
- The first term of a G.P. is 1. The sum of the third term and fifth term is 90.
Find the common ratio of G.P.
- The sum of three numbers in G.P. is 56. If we subtract 1, 7, 21 from these numbers in that order, we obtain an arithmetic progression. Find the numbers.
Solution 👉 Click Here
- A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.
Solution 👉 Click Here
- If
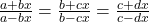 (x≠ 0), then show that a, b, c and d are in G.P.
(x≠ 0), then show that a, b, c and d are in G.P.
Solution 👉 Click Here
Solution
Given that
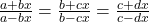
Using componendo dividendo rule, we get
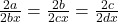
or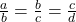
This shows that a,b,c, d are in GP
This completes the solution.
- Let S be the sum, P the product and R the sum of reciprocals of n terms in a G.P.
Prove that
 .
.
Solution 👉 Click Here
- If a, b, c, d are in GP, prove that
 are in GP
are in GP
Solution 👉 Click Here
- If a and b are the roots of
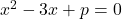 and c, d are roots of
and c, d are roots of  ,
where a, b, c, d form a GP. Prove that (q + p) : (q – p) = 17:15.
,
where a, b, c, d form a GP. Prove that (q + p) : (q – p) = 17:15.
Solution 👉 Click Here
- The ratio of the A.M. and G.M. of two positive numbers a and b, is m : n. Show that
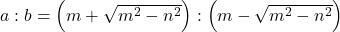
Solution 👉 Click Here
- Find the sum of the following series up to n terms:
(i) 5 + 55 +555 + …
(ii) 0.6 +0.66 +0.666+…
- Find the 20th term of the series 2 × 4 + 4 × 6 + 6 × 8 + ... + n terms.
Solution 👉 Click Here
Solution
Find the 20th term of the series is
(20th term of 2,4,6,..)*(20th term of 4,6,8,.. )
This completes the solution.
- A farmer buys a used tractor for Rs 12000. He pays Rs 6000 cash and agrees to
pay the balance in annual instalments of Rs 500 plus 12% interest on the unpaid
amount. How much will the tractor cost him?
- Bidhan buys a scooter for Rs 22000. He pays Rs 4000 cash and agrees to pay the balance in annual instalment of Rs 1000 plus 10% interest on the unpaid amount. How much will the scooter cost him?
Solution 👉 Click Here
Solution
The unpaid amount forms a sequence given as
18000, 17000,16000,...,1000 for 18 installments (18 terms)
1000, 2000,3000,...,18000 for 18 installments (18 terms)
Using formula, the sum of unpaid amounts is
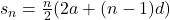
or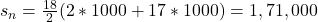
So, the interset paiid is
10% of 171000=17100
So, the cost of the scooter is
22000+17100=39100
This completes the solution.
- A person writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with instruction that they move the chain similarly. Assuming that the chain is not broken and that it costs 50 paise to mail one letter. Find the amount spent on the postage when 8th set of letter is mailed.
Solution 👉 Click Here
Solution
Given that, one person writes letter to his 4 friends, aagain, each of these 4 friends will write letter to their 4 friends. So, the number of letters written here will be 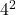 . This continues....
. This continues....
So, the number forms a GP given as
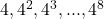
Here, a=4,r=4,n=8
So,
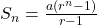
or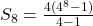
or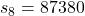
Now, cost to mail the letters is
0.5*87380=Rs 43690
This completes the solution.
- A man deposited Rs 10000 in a bank at the rate of 5% simple interest annually. Find the amount in 15th year since he deposited the amount and also calculate the total amount after 20 years.
- A manufacturer reckons that the value of a machine, which costs him Rs. 15625, will depreciate each year by 20%. Find the estimated value at the end of 5 years.
- 150 workers were engaged to finish a job in a certain number of days. 4 workers dropped out on second day, 4 more workers dropped out on third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed.
Solution 👉 Click Here
Solution
Let us assume that, 150 workers finish a work in x days.
Then, according to question
Number of workers working in each days are respectively
150,146,142,......and it continues up to (x+8) terms [sine 8 more days are required]
This shows that, the numbers are in A.P. with first term 150, common difference -4 and number of terms as (x+8)
So,
![Rendered by QuickLaTeX.com 150x= \frac{n}{2} [2a+(n-1)d]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-08a29017b08020cab9733a6d832312bb_l3.png)
or![Rendered by QuickLaTeX.com 150x= \frac{x+8}{2} [2.150+(x+8-1)(-4)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-9f63ac7300d0d2f7cb6b61f3ca15c636_l3.png)
orx=17 or x=-32
or x=17days can NOT be nagative
This completes the solution.
EXERCISE 8.2 [NCERT, page 145]
- Find the 20th and nth terms of the G.P.
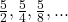
Solution 👉 Click Here
- Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2.
Solution 👉 Click Here
- The 5th, 8th and 11th terms of a G.P. are p, q and s, respectively. Show that
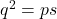 .
.
Solution 👉 Click Here
- The 4th term of a G.P. is square of its second term, and the first term is – 3.
Determine its 7th term.
Solution 👉 Click Here
- Which term of the following sequences:
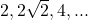 is 128 ?
is 128 ?
Solution 👉 Click Here
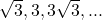 is 729 ?
is 729 ?
Solution 👉 Click Here
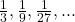 is
is 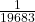
Solution 👉 Click Here
- For what values of x, the numbers
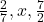 are in G.P.?
are in G.P.?
Solution 👉 Click Here
Find the sum to indicated number of terms in each of the geometric progressions in Exercises 7 to 10:
- 0.15, 0.015, 0.0015, ... 20 terms
Solution 👉 Click Here
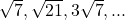 n terms
n terms
Solution 👉 Click Here
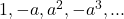 n terms (if a≠-1)
n terms (if a≠-1)
Solution 👉 Click Here
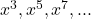 n terms (if
n terms (if 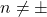 1)
1)
Solution 👉 Click Here
- Evaluate
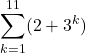
Solution 👉 Click Here
- The sum of first three terms of a G.P. is
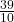 and their product is 1. Find the common ratio and the terms.
and their product is 1. Find the common ratio and the terms.
- How many terms of G.P.
 , … are needed to give the sum 120?
, … are needed to give the sum 120?
- The sum of first three terms of a G.P is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the G.P.
- Given a G.P. with a = 729 and 7th term 64, determine
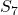 .
.
- Find a G.P. for which sum of the first two terms is – 4 and the fifth term is 4 times the third term.
- If the 4th, 10th and 16th terms of a G.P. are x, y and z, respectively. Prove that x, y, z are in G.P.
- Find the sum to n terms of the sequence, 8, 88, 888, 8888… .
- Find the sum of the products of the corresponding terms of the sequences 2, 4, 8,16, 32 and
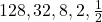
- Show that the products of the corresponding terms of the sequences
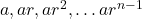 and
and 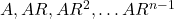 form a G.P, and find the common ratio.
form a G.P, and find the common ratio.
- Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the 4th by 18.
- If the pth, qth and rth terms of a G.P. are a, b and c, respectively. Prove that
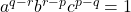 .
.
Solution 👉 Click Here
- If the first and the nth term of a G.P. are a and b, respectively, and if P is the product of n terms, prove that
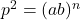 .
.
Solution 👉 Click Here
- Show that the ratio of the sum of first n terms of a G.P. to the sum of terms from
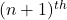 to
to  term is
term is 
- If a, b, c and d are in G.P. show that
 .
.
- Insert two numbers between 3 and 81 so that the resulting sequence is G.P.
- Find the value of n so that
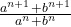 may be the geometric mean between a and b.
may be the geometric mean between a and b.
- The sum of two numbers is 6 times their geometric mean, show that numbers are in the ratio
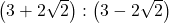
- If A and G be A.M. and G.M., respectively between two positive numbers, prove that the numbers are
- The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour ?
- What will Rs 500 amounts to in 10 years after its deposit in a bank which pays annual interest rate of 10% compounded annually?
- If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation.
- Determine the nature of roots of each of the following equations

Solution 👉 Click Here
Solution :1a
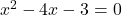
Solution 👉 Click Here
Solution :1b
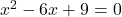
Solution 👉 Click Here
Solution :1c
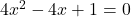
Solution 👉 Click Here
Solution :1d

Solution 👉 Click Here
Solution :1e
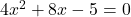
Solution 👉 Click Here
Solution :1f
- For what values of p will the equation
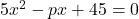 ?
?
Solution 👉 Click Here
Solution :2
- if the equation
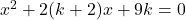 has equal roots, find k.
has equal roots, find k.
Solution 👉 Click Here
Solution :3
- For what value of a will the equation
 have equal roots?
have equal roots?
Solution 👉 Click Here
Solution :4
- If the roots of the equation
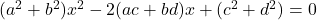 are equal, then show that
are equal, then show that 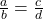
Solution 👉 Click Here
Solution :5
- Show that the roots of the equation
 will be equal, if either
will be equal, if either  or
or 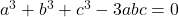
Solution 👉 Click Here
Solution :6
- If
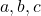 are rational and
are rational and 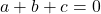 , show that the roots
, show that the roots  are rational.
are rational.
Solution 👉 Click Here
Solution :7
- Prove that the roots of the equation
 are real for all values of k.
are real for all values of k.
Solution 👉 Click Here
Solution :8
- Show that the roots of the equation
 are imaginary.
are imaginary.
Solution 👉 Click Here
Solution :9
- If the roots of the quadratic equation
 are real and unequal, prove that the roots of the equation
are real and unequal, prove that the roots of the equation 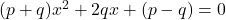 are imaginary
are imaginary
Solution 👉 Click Here
Solution :10
- From the equation whose roots are
- 3,-2
Solution 👉 Click Here
Solution :1a
- -5,4
Solution 👉 Click Here
Solution :1b
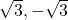
Solution 👉 Click Here
Solution :1c
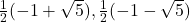
Solution 👉 Click Here
Solution :1d
- -3+5i,-i-5i
Solution 👉 Click Here
Solution :1e
- a+ib,a-ib
Solution 👉 Click Here
Solution :1f
-
- Find a quadratic equation whose roots are twice the roots of
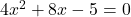
Solution 👉 Click Here
Solution :2a
- Find a quadratic equation whose roots are reciprocals of the roots of
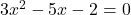
Solution 👉 Click Here
Solution :2(b)
- Find a quadratic equation whose roots are greater by h than the roots of
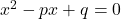
Solution 👉 Click Here
Solution :2(c)
- Find a quadratic equation whose roots are the squares of the roots of
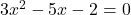
Solution 👉 Click Here
Solution :2(d)
- Find a quadratic equation with rational coefficients one of whose roots is
- 4+3i
Solution 👉 Click Here
Solution :3a
-
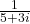
Solution 👉 Click Here
Solution :3b
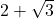
Solution 👉 Click Here
Solution :3c
- Find the value of k so that the equation
 has one root 3
has one root 3
Solution 👉 Click Here
Solution :4a
 has roots whose sum is equal to 6
has roots whose sum is equal to 6
Solution 👉 Click Here
Solution :4b
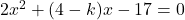 has roots equal but opposite in sign
has roots equal but opposite in sign
Solution 👉 Click Here
Solution :4c
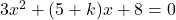 has roots numerically equal but opposite in sign
has roots numerically equal but opposite in sign
Solution 👉 Click Here
Solution :4d
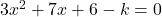 has one root equal to zero
has one root equal to zero
Solution 👉 Click Here
Solution :4e
 has the reciprocal roots
has the reciprocal roots
Solution 👉 Click Here
Solution :4f
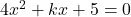 has roots whose difference is
has roots whose difference is 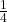
Solution 👉 Click Here
Solution :4g
- Show that -1 is a root of the equation
 x^2+(2a-b-c)x+(c+a-2b)=0\). Find the other root.
x^2+(2a-b-c)x+(c+a-2b)=0\). Find the other root.
Solution 👉 Click Here
Solution :5
- Find the value of m for which the equation
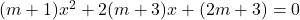 will have (a) reciprocal roots (b) one root zero.
will have (a) reciprocal roots (b) one root zero.
Solution 👉 Click Here
Solution :6
- If the roots of the equation
 differ by 1, prove that
differ by 1, prove that 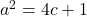
Solution 👉 Click Here
Solution :7
- If
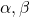 are the roots of the equation
are the roots of the equation 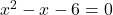 , find the equation whose roots are
, find the equation whose roots are
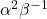 and
and 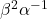
Solution 👉 Click Here
Solution :8a
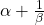 and
and 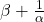
Solution 👉 Click Here
Solution :8(b)
- If
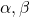 are the roots of the equation
are the roots of the equation 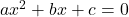 , find the equation whose roots are
, find the equation whose roots are
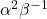 and
and 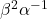
Solution 👉 Click Here
Solution :9a
 and
and 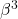
Solution 👉 Click Here
Solution :9b
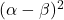 and
and 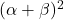
Solution 👉 Click Here
Solution :9c
- the reciprocal of the roots of given equation
Solution 👉 Click Here
Solution :9d
-
- If the roots of the equation
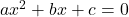 be in the ratio of 3:4, prove that
be in the ratio of 3:4, prove that 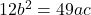
Solution 👉 Click Here
Solution :10a
- If one root of the equation
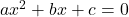 be four times the other root, show that
be four times the other root, show that 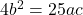
Solution 👉 Click Here
Solution :10b
- For what values of m, the equation
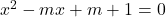 may have its root in the ratio 2:3
may have its root in the ratio 2:3
Solution 👉 Click Here
Solution :10c
-
- If
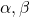 are the roots of the equation
are the roots of the equation 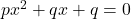 , prove that
, prove that 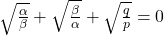
Solution 👉 Click Here
Solution :11a
- If roots of the equation
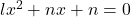 be in the ratio of p:q, prove that
be in the ratio of p:q, prove that 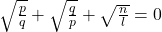
Solution 👉 Click Here
Solution :11b
- If one root of the equation
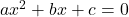 be square of the other root, prove that
be square of the other root, prove that 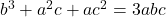
Solution 👉 Click Here
Solution :12
- Show that each pair of following equations has a common root
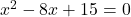 and
and 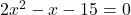
Solution 👉 Click Here
Solution :1(a)
Given quadratic equations are
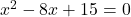 and
and 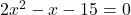
Comparing with
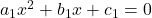
and
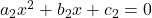
, we get
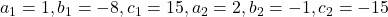
We know that, condition for two quadratic equations having a common root is
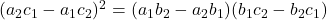
or
![Rendered by QuickLaTeX.com [2.(15)-1(-15)]^2 = [1(-1)-2(-8)] [(-8)(-15)-(-1)(15)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-6e5edf241f01c8d46ae741faf69221df_l3.png)
or
![Rendered by QuickLaTeX.com [30+15]^2 = [-1+16] [120+15]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-50472ad5baeff0a916e57edc3ab700da_l3.png)
or
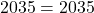
Thus,
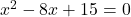
and
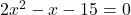
has a common root.
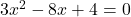 and
and 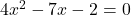
Solution 👉 Click Here
Solution :1(b)
Given quadratic equations are
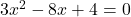 and
and 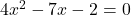
Comparing with
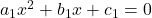
and
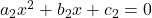
, we get
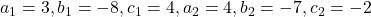
We know that, condition for two quadratic equations having a common root is
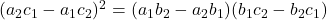
or
![Rendered by QuickLaTeX.com [(4)(4)-(3)(-2)]^2 = [(3)(-7)-(4)(-8)] [(-8)(-2)-(-7)(4)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-c45b3ffc9bf56981a9b23eec29857753_l3.png)
or
![Rendered by QuickLaTeX.com [16+6]^2 = [-21+32] [16+28]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-8e971129777a8bb1584a0691b043f84c_l3.png)
or
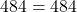
Thus,
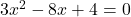
and
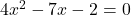
has a common root.
- Find the value of p so that each pair of the equations may have one root common
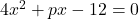 and
and 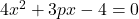
Solution 👉 Click Here
Solution :2(a)
Given quadratic equations are
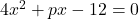 and
and 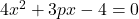
Comparing with
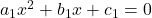
and
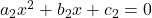
, we get
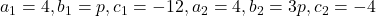
We know that, condition for two quadratic equations having a common root is
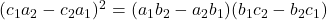
or
![Rendered by QuickLaTeX.com [(-12)(4)-(-4)(4)]^2 = [(4)(3p)-(4)(p)] [(p)(-4)-(3p)(-12)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-b7ca65ba70693d5d8e8456784ec4e446_l3.png)
or
![Rendered by QuickLaTeX.com [-48+16]^2 = [12p-4p] [-4p+36p]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-fa39f4792911a8f3fd181334da8e903f_l3.png)
or
![Rendered by QuickLaTeX.com [-32]^2 = [8p] [32p]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-5e18f4fd20b56446dc8da6b18034048a_l3.png)
or
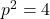
or
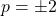
Thus,fo
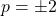
, given pair of the equations may have one root common
 and
and 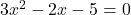
Solution 👉 Click Here
Solution :2(b)
Given quadratic equations are
 and
and 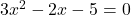
Comparing with
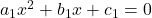
and
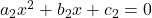
, we get
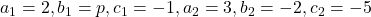
We know that, condition for two quadratic equations having a common root is
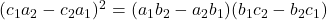
or
![Rendered by QuickLaTeX.com [(-1)(3)-(-5)(2)]^2 = [(2)(-2)-(3)(p)] [(p)(-5)-(-2)(-1)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-9011cc33e0f07f701b065ecce4e2ca10_l3.png)
or
![Rendered by QuickLaTeX.com [-3+10]^2 = [-4-3p] [-5p-2]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-1a2f065c1d7f0ed71f4916d86cbe6a4a_l3.png)
or
![Rendered by QuickLaTeX.com [7]^2 = [4+3p] [2+5p]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-446f7e851bfb1530acf29c277a4677a1_l3.png)
or
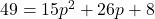
or
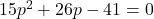
or
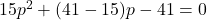
or
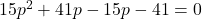
or
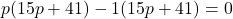
or
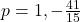
Thus,fo
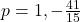
, given pair of the equations may have one root common
- If the quadratic equations
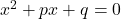 and
and 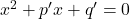 have common roots show that it must be either
have common roots show that it must be either  or
or 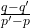
Solution 👉 Click Here
Solution :3
Given quadratic equations are
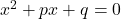 and
and 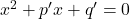
Comparing with
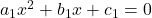
and
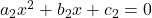
, we get
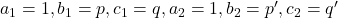
We know that, condition for two quadratic equations having a common root is
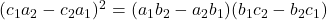
or
![Rendered by QuickLaTeX.com [(q)(1)-(q')(1)]^2 = [(1)(p')-(1)(p)] [(p)(q')-(p')(q)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-840c590133e613937c7ece8dcaf556d9_l3.png)
or
![Rendered by QuickLaTeX.com [q-q']^2 = [p'-p] [pq'-p'q]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-eaf1443a4d1fbe0cc123547c13ec5a90_l3.png)
or
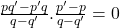
or
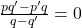 or
or 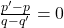
or
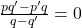 or
or 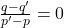
Thus,
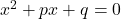
and
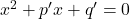
have one root common if
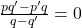
or
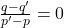
- If the quadratic equations
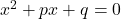 and
and 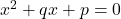 have common roots show that it must be either
have common roots show that it must be either 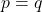 or
or 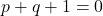
Solution 👉 Click Here
Solution :4
Given quadratic equations are
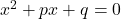 and
and 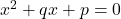
Comparing with
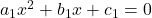
and
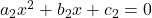
, we get
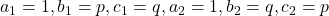
We know that, condition for two quadratic equations having a common root is
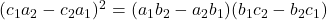
or
![Rendered by QuickLaTeX.com [(q)(1)-(p)(1)]^2 = [(1)(q)-(1)(p)] [(p)(p)-(q)(q)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-61aa588e94dbb9f9fe44912038ad2faf_l3.png)
or
![Rendered by QuickLaTeX.com [q-p]^2 = [q-p] [p^2-q^2]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-a831d8ccb663421da517d1bfd9e5fb93_l3.png)
or
![Rendered by QuickLaTeX.com (q-p) [(q-p)- (p^2-q^2)]=0](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-6c62fd1b7db9938b4afee1b8c9837b97_l3.png)
or
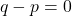 or
or 
Thus,
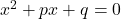
and
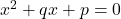
have one root common if
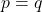
or

- If the quadratic equations
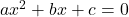 and
and 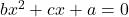 have common roots show that it must be either
have common roots show that it must be either 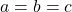 or
or 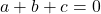
Solution 👉 Click Here
Solution :5
Given quadratic equations are
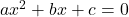 and
and 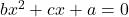
Comparing with
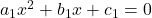
and
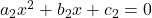
, we get
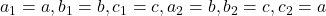
We know that, condition for two quadratic equations having a common root is
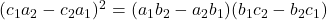
or
![Rendered by QuickLaTeX.com [(c)(b)-(a)(a)]^2 = [(a)(c)-(b)(b)] [(b)(a)-(c)(c)]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-b2c292212cd695b8f3c6bbc8292fb172_l3.png)
or
![Rendered by QuickLaTeX.com [bc-a^2]^2 = [ca-b^2] [ab-c^2]](https://mean.edu.np/wp-content/ql-cache/quicklatex.com-668ae80b9cd6a7d00ef3839e9bdaf854_l3.png)
or
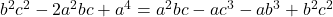
or
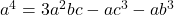
or
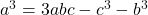
or
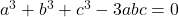
or
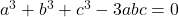
or
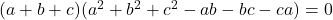
or
Either 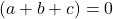 or
or 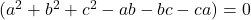
or
Either 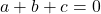 or
or 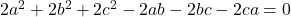
or
Either 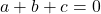 or
or 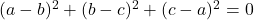
or
Either 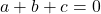 or
or 
or
Either 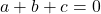 or
or 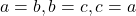
or
Either 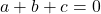 or
or 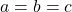
Thus,
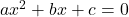
and
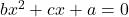
have one root common if
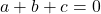
or
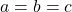
- Prove that if the equations
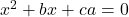 and
and 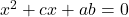 have a common root, their other root will satisfy
have a common root, their other root will satisfy 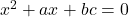
Solution 👉 Click Here
Solution :6
Given quadratic equations are
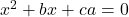 and
and 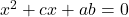
Let
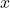
be the common solution of the equations
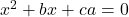
and
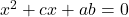
then
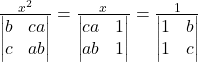
Comparing first two, we get
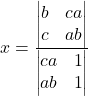
or
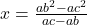
or
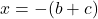
Again, comparing last two, we get
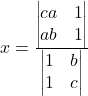
or
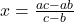
or

Using both values of x, we get
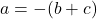
or
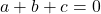
Now, suppose
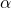
be the other root of
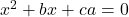
, then

or
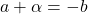
or
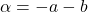
Next, suppose
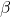
be the other root of
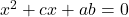
, then
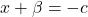
or
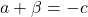
or
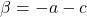
Now, new quadratic equation containing other roots
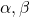
is given by
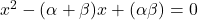
or
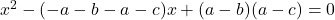
or
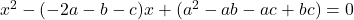
or
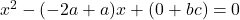
or
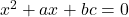
![]() and define as follows.
and define as follows.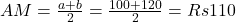
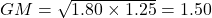 , the average growth is 50%
, the average growth is 50%
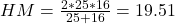
 liter
liter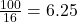 liter
liter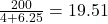

 Arithmetic mean is greater than geometric mean and harmonic mean, and geometric mean is greater than harmonic mean.
Arithmetic mean is greater than geometric mean and harmonic mean, and geometric mean is greater than harmonic mean. ![]()
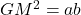


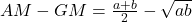
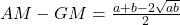
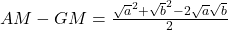
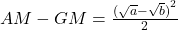
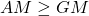 (1)
(1)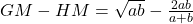
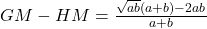
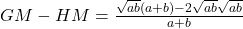
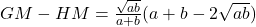
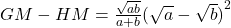
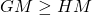 (2)
(2)
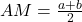

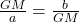
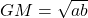
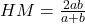
 , OD=
, OD= , so we have
, so we have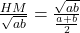

![]()
![]()
![]() and define as follows.
and define as follows.![]()
![]()
![]() item
item![]() item
item![]() item
item![]() hundreds
hundreds![]() , thus, based on the formula, the Median class is
, thus, based on the formula, the Median class is ![]() item
item![]() item
item![]() item
item![]() item lies in the
item lies in the ![]() of 125, thus
of 125, thus![]()
![]()
![]()
![]() , thus, based on the formula, the Median class is
, thus, based on the formula, the Median class is ![]() item
item![]() item
item![]() item
item![]() item lies in the
item lies in the ![]() of 10, thus
of 10, thus![]()
![]()
![]()
![]() does not lie in the class
does not lie in the class ![]() as instructed for inclusive data groupings, teaches need to encourage the usual rules for computing.
as instructed for inclusive data groupings, teaches need to encourage the usual rules for computing.![]() and define as follows.
and define as follows.![]() . Thus,
. Thus, ![]()
![]()
![]()
![]() , however three are big frequencies around 22, thus we use analytical method to find the Mode.
, however three are big frequencies around 22, thus we use analytical method to find the Mode.