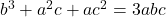Skip to content
- From the equation whose roots are
- 3,-2
Solution 👉 Click Here
Solution :1a
- -5,4
Solution 👉 Click Here
Solution :1b
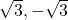
Solution 👉 Click Here
Solution :1c
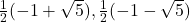
Solution 👉 Click Here
Solution :1d
- -3+5i,-i-5i
Solution 👉 Click Here
Solution :1e
- a+ib,a-ib
Solution 👉 Click Here
Solution :1f
-
- Find a quadratic equation whose roots are twice the roots of
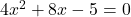
Solution 👉 Click Here
Solution :2a
- Find a quadratic equation whose roots are reciprocals of the roots of
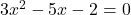
Solution 👉 Click Here
Solution :2(b)
- Find a quadratic equation whose roots are greater by h than the roots of
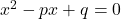
Solution 👉 Click Here
Solution :2(c)
- Find a quadratic equation whose roots are the squares of the roots of
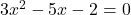
Solution 👉 Click Here
Solution :2(d)
- Find a quadratic equation with rational coefficients one of whose roots is
- 4+3i
Solution 👉 Click Here
Solution :3a
-
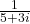
Solution 👉 Click Here
Solution :3b
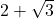
Solution 👉 Click Here
Solution :3c
- Find the value of k so that the equation
 has one root 3
has one root 3
Solution 👉 Click Here
Solution :4a
 has roots whose sum is equal to 6
has roots whose sum is equal to 6
Solution 👉 Click Here
Solution :4b
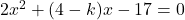 has roots equal but opposite in sign
has roots equal but opposite in sign
Solution 👉 Click Here
Solution :4c
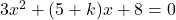 has roots numerically equal but opposite in sign
has roots numerically equal but opposite in sign
Solution 👉 Click Here
Solution :4d
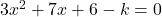 has one root equal to zero
has one root equal to zero
Solution 👉 Click Here
Solution :4e
 has the reciprocal roots
has the reciprocal roots
Solution 👉 Click Here
Solution :4f
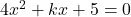 has roots whose difference is
has roots whose difference is 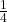
Solution 👉 Click Here
Solution :4g
- Show that -1 is a root of the equation
 x^2+(2a-b-c)x+(c+a-2b)=0\). Find the other root.
x^2+(2a-b-c)x+(c+a-2b)=0\). Find the other root.
Solution 👉 Click Here
Solution :5
- Find the value of m for which the equation
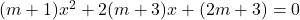 will have (a) reciprocal roots (b) one root zero.
will have (a) reciprocal roots (b) one root zero.
Solution 👉 Click Here
Solution :6
- If the roots of the equation
 differ by 1, prove that
differ by 1, prove that 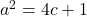
Solution 👉 Click Here
Solution :7
- If
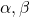 are the roots of the equation
are the roots of the equation 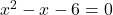 , find the equation whose roots are
, find the equation whose roots are
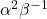 and
and 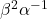
Solution 👉 Click Here
Solution :8a
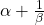 and
and 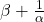
Solution 👉 Click Here
Solution :8(b)
- If
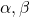 are the roots of the equation
are the roots of the equation 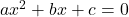 , find the equation whose roots are
, find the equation whose roots are
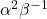 and
and 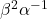
Solution 👉 Click Here
Solution :9a
 and
and 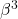
Solution 👉 Click Here
Solution :9b
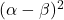 and
and 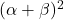
Solution 👉 Click Here
Solution :9c
- the reciprocal of the roots of given equation
Solution 👉 Click Here
Solution :9d
-
- If the roots of the equation
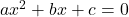 be in the ratio of 3:4, prove that
be in the ratio of 3:4, prove that 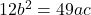
Solution 👉 Click Here
Solution :10a
- If one root of the equation
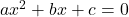 be four times the other root, show that
be four times the other root, show that 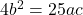
Solution 👉 Click Here
Solution :10b
- For what values of m, the equation
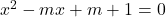 may have its root in the ratio 2:3
may have its root in the ratio 2:3
Solution 👉 Click Here
Solution :10c
-
- If
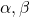 are the roots of the equation
are the roots of the equation 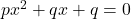 , prove that
, prove that 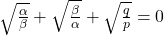
Solution 👉 Click Here
Solution :11a
- If roots of the equation
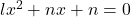 be in the ratio of p:q, prove that
be in the ratio of p:q, prove that 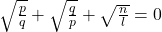
Solution 👉 Click Here
Solution :11b
- If one root of the equation
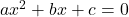 be square of the other root, prove that
be square of the other root, prove that 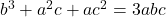
Solution 👉 Click Here
Solution :12
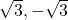
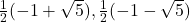
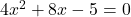
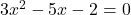
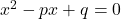
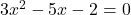
 has one root 3
has one root 3 has roots whose sum is equal to 6
has roots whose sum is equal to 6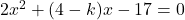 has roots equal but opposite in sign
has roots equal but opposite in sign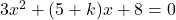 has roots numerically equal but opposite in sign
has roots numerically equal but opposite in sign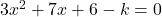 has one root equal to zero
has one root equal to zero has the reciprocal roots
has the reciprocal roots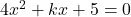 has roots whose difference is
has roots whose difference is 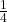
 x^2+(2a-b-c)x+(c+a-2b)=0\). Find the other root.
x^2+(2a-b-c)x+(c+a-2b)=0\). Find the other root.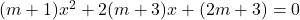 will have (a) reciprocal roots (b) one root zero.
will have (a) reciprocal roots (b) one root zero. differ by 1, prove that
differ by 1, prove that 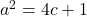
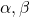 are the roots of the equation
are the roots of the equation 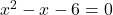 , find the equation whose roots are
, find the equation whose roots are
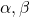 are the roots of the equation
are the roots of the equation 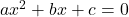 , find the equation whose roots are
, find the equation whose roots are
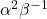 and
and 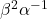
 and
and 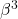
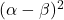 and
and 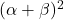
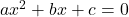 be in the ratio of 3:4, prove that
be in the ratio of 3:4, prove that 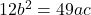
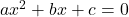 be four times the other root, show that
be four times the other root, show that 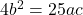
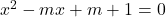 may have its root in the ratio 2:3
may have its root in the ratio 2:3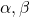 are the roots of the equation
are the roots of the equation 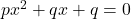 , prove that
, prove that 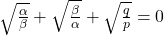
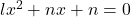 be in the ratio of p:q, prove that
be in the ratio of p:q, prove that 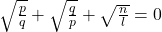
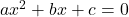 be square of the other root, prove that
be square of the other root, prove that